
Overview of a general flat-fielding problem and description of its solution by Munipack.
Munipack implements its own flat-field algorithm on base of the standard photometry calibration rather than commonly used methods (they uses of median of scaled flat-fields). The presented approach enables to reach the maximal possible accuracy which is limited by only statistical noise of the light. The approach has been not found in any available literature.
Although a correct flat-field is the crucial tool for reaching of suitable photometry accuracy, the care of acquiring and processing of flat-fields is not commonly appropriate. This is especially true for any flat-field post-processing.
A capacity of common semi-conductor detectors is limited on values, say, 200k counts per pixels. A good flat-field has its mean level about half of full range, eg. 100k counts which gives its relative accuracy on value √100k / 100k ≈ 0.003 per pixel, if Poisson distribution can by considered. So for a star which occupy about ten pixels (3×3), one will have a relative deviation over 0.01 magnitude due to the flat-field. A small error in flat-field determination can lead to measurable deviations of results.
To improve the precision, increase of a capacity of detectors can help, but it have technical limitations. Also, it will not suppress different light sensitivity of pixels including all the optical path. In this case, the feasible way is averaging of frames as provides Munipack flat utility.
Mean levels of flat-fields, captured using of an unstable light source (during twilight), are unequal. As a consequence, a direct average of that flat-fields is impossible.
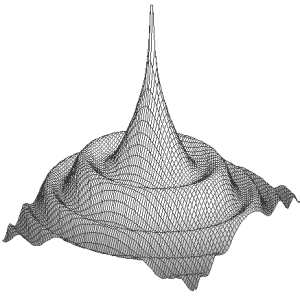
A common solution of the trouble is an initial normalisation of flat-fields on an equal intensity level. The approach key difficulty is the determination of a mean level of every frame. Single frame values has no Normal distribution which is leading to a staticticaly poor definition of the average level.

The difficulty comes due to the folded surface of flat-fields. While it is possible to compute a mean level, the estimate will not be optimal or accurate due to blending of statistical distributions: the light noise and the surface of flat-field itself.
The crucial point of Munipack approach is decomposition of flat-field frames on single, independent pixels. These pixels, having the same position and collected over all frames, can be considered as sources of the light like stars; a star calibration procedure can be subsequenty used. Reference sources are initially unknown, fortunately, they can be estimated by iterations.
Munipack implements two-phase algorithm which determine a rough flat-field during the first phase (equivalent to common practice). In the second phase, it determines the mean level of individual frames by scaling on to the rough initial flat approximation. The second phase of the approach works with Normally distributed data giving accurate, reliable and statistically correct results.

The developed algorithm solves a non-linear implicit equation for all pixels of the final flat-field. The approach is a variant of photon calibration, the reference photon sources are iteratively established during the computation.
There is a list of rules, summarising of my long time experiences with flat-fielding, which I recommends for flat-fielding:
Flat-field manual, Photometry corrections. Standing on the shoulders of giants.