
A mapping of high dynamical range of astronomical images to limited range of display devices is crucial for best user visual experience. There are described rendering methods used by Munipack.
The dynamical range of a standard CCD camera is over 65 thousand. When any taken image is processed or single exposures are composed, its range can be expanded. Also frequently the images can be calibrated to a physical quantities. Therefore the range of images must be supposed to be unlimited (usually in interval zero to positive infinity). Moreover, a typical processed image has dynamical range spread over many orders. Unfortunately, the display range of conventional device is just only 256 levels (limits by both display devices and by software). Methods for mapping of an principially unlimited dynamical range to a limited range are discussed here.
By method, it is possible to use global or local mapping techniques. The global mapping stretch full range to a predefined range by a global transformation function (acting on all pixels equivalently). The local mapping adapts the transformation according to values actual pixels. The local technique would remove large structures from image and shows only local rapid changes. Local techniques simulates perception of human eye. Munipack currently implements only global techniques.
The linear mapping simply converts a wide range (represented usually by numbers from the real set) to a limited interval with linear scaling and cut-off. The linear scaling is represented by
i = B + S · I,
where i is a display intensity, I is an original intensity. The parameter B (black level) sets the intensity level in an original picture corresponding to black colour on the display. The slope S determines the intensity range which will be displayed. The intensities out of display range are cut-offed. Lower intensities to black and higher ones to white.
The parameters are not orthogonal. The change of both will brighten or darken the picture but the results will be different. There is no known widely used orthogonal set of parameters.






The direct use of contrast/luminosity parameters for adjusting of range is not possible due to principal difference of both operations.
There is an weak analogy between black and slope parameters and widely known contrast and brightness parameters. The black corresponds to brightness and contrast corresponds to slope. The formal definition and usage of both twines of parameters is different. On the other side, the practical usage of both parameters is similar.
Munipack has included empirical estimate of parameters on base of descriptive statistics.
Lets median of selected pixels of an image is
Dmed = med Dij,
and median of absolute deviations of the image is
Dmad= med |Dij - Dmed|,
than the parameters are initially estimated to
B = Dmed - k Dmad,
S = 1 / w Dmad.
Ones are choose to k = 0, w = 30.
The estimator and parameters has been determined empirically by visually comparing of set of images with different parameters. The algorithm perfectly works on images with Gaussian-like histogram. The prototype of the images can be a sparse stars sky field. The histogram is mostly composed from the noise of the sky. Stars have just only marginally importance. Images with non-Gaussian histogram are estimated poorly by the way.
The estimator uses just only a few thousands of pixels in selected regular grid covering of full frame. The median is used as estimator of mean. The use of arithmetical mean does not work at all because one is too sensitive to outliners.
The values prescaled by the above linear transformation can be directly used in more general transformation:
i' = f0 · f(i) + z,
where f0 and scales and z vertically shifts the function. Available functions are:
| Function | Description |
|---|---|
| asinh | Wide range without background noise. Intended for general usage. Suggested by Lupton et al. (2004) |
| log | Simulates magnitudes. Emphasizes details on background. On high levels similar to asinh. |
| sqrt | Similar to log. Inspired by ds9 (saoimage). |
| gamma | Gamma function with power 1/4.2 (as in sRGB). Just only for comparison. |
| normal | Normal ‒ Gaussian ‒ distribution function (integral of Gaussian hat). As the simulation of gradation curve of classical photography. |
| logistic | Logistic function. The similar usage as for normal |
| atan | Arc tan. The similar usage as for normal |
| square | Square has opposite curvature to all others. Emphasizes low-contrast details in noise background. |



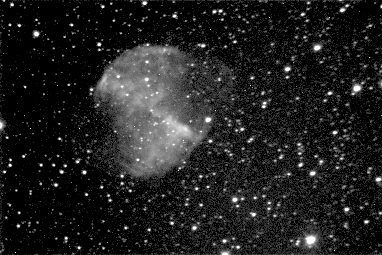
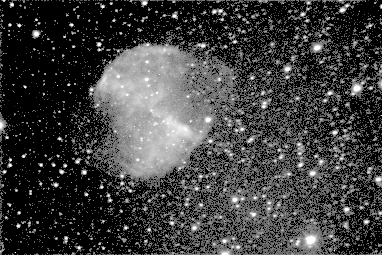

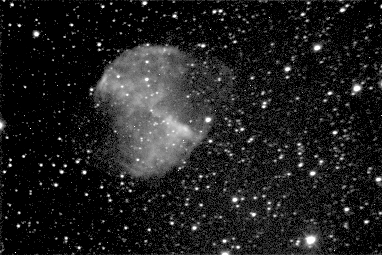
Mostly (all) widely used displays are using the gamma correction. The correction transforms already mapped i so response on linear stimulus in input intensity is linear response (humans perception).
The gamma correction takes the form
i' = i1/γ,
where γ is 4.2 for sRGB and 4.0 for AdobeRGB display. Without the correction, images appears too dim.

In case of colour images, the scaled component is not more directly the intensity but the L component of CIE Luv color space:
I ≡ L = 116 Y1/3 - 16.
The colours itself are untouched. The scaled value I' and colour is than transformed back to CIE XYZ. The reason of the technique is saving of colours. Without the transformation colours are deformed and does not corresponds to human perception.




Full access to tone tuning is available via a graphical interface.
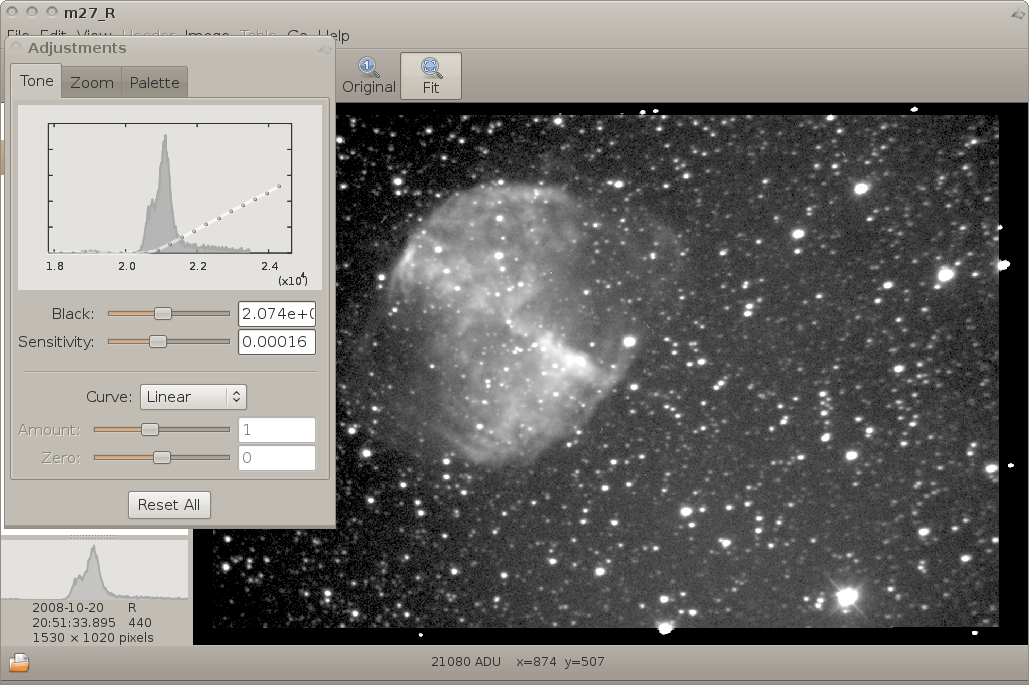
The algorithm as is implemented in xmunipack/fitsimage.cpp.